Academic pursuits
Here’s where I put up descriptions and musings about some topics that I professionally (as in get paid to) worry about. Please refer to my CV in the “About” section for a list of publications.
Temporal modes
(Coming soon)
 The quantum wave functions of photons are
essentially identical to the classical mode functions they populate.
This allows for wave-packet quantization of light, and opens up a “new”
Hilbert space for information storage, retrieval, and manipulation. In
simple terms, two photons with the same central frequency and
time-of-arrival, with matching polarizations and transverse spatial-beam
profiles, can still have orthogonal pulse shapes, i.e. complex envelope
functions of their modes in the direction of propagation. These have
been the central topic of my grad-research.
The quantum wave functions of photons are
essentially identical to the classical mode functions they populate.
This allows for wave-packet quantization of light, and opens up a “new”
Hilbert space for information storage, retrieval, and manipulation. In
simple terms, two photons with the same central frequency and
time-of-arrival, with matching polarizations and transverse spatial-beam
profiles, can still have orthogonal pulse shapes, i.e. complex envelope
functions of their modes in the direction of propagation. These have
been the central topic of my grad-research.
Nonlinear wave mixing
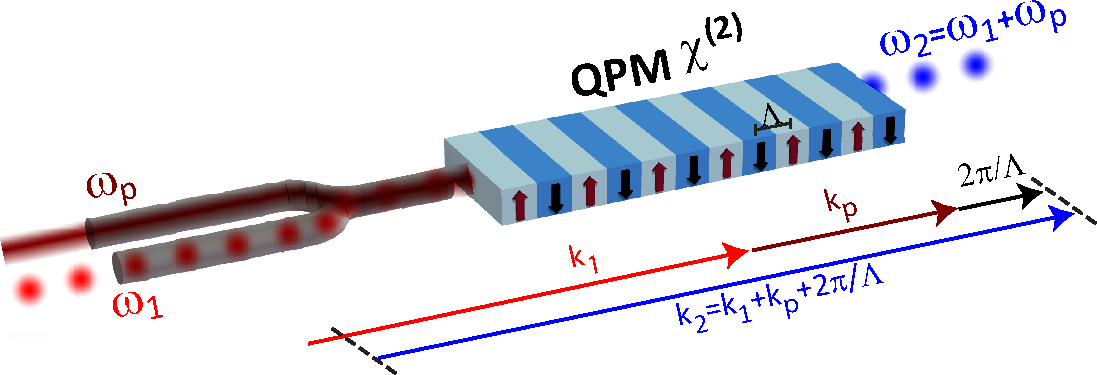 Image Source. Pedagogically speaking, interference in
radiation patterns of dipole antennas is an amazing technical topic for
instruction. It spans a diverse range of phenomena and relies on very
rudimentary Euclidean visualization skills in the pupils. I’ve been
experimenting on combining this with basic concepts of Fourier
transforms to create a self-contained teaching module for nonlinear wave
mixing in non-resonantly excited media. My continued efforts will be
updated in this tab.
Image Source. Pedagogically speaking, interference in
radiation patterns of dipole antennas is an amazing technical topic for
instruction. It spans a diverse range of phenomena and relies on very
rudimentary Euclidean visualization skills in the pupils. I’ve been
experimenting on combining this with basic concepts of Fourier
transforms to create a self-contained teaching module for nonlinear wave
mixing in non-resonantly excited media. My continued efforts will be
updated in this tab.
Neutrino rumble
(Coming soon)
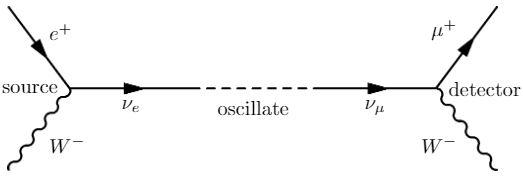 Image Source. In the standard model of physics,
neutrinos come in three flavors: electron-, muon-, and tau-neutrino. But
the flavors that are produced in processes aren’t necessarily the
flavors that are detected (if indeed we can separate these two
occurences as different events). That is because the mass eigenstates
and flavor eigenstates are not identical! I’ve been under the delusion
(for some time now) of this being exploitable in an experiment that
could reveal the absolute masses of said states (which are still not
known). My quixotic exploration of this has brought up some interesting
questions about the nature of interaction and the measurement problem.
I’ll try and keep this tab updated as and when new things come up.
Image Source. In the standard model of physics,
neutrinos come in three flavors: electron-, muon-, and tau-neutrino. But
the flavors that are produced in processes aren’t necessarily the
flavors that are detected (if indeed we can separate these two
occurences as different events). That is because the mass eigenstates
and flavor eigenstates are not identical! I’ve been under the delusion
(for some time now) of this being exploitable in an experiment that
could reveal the absolute masses of said states (which are still not
known). My quixotic exploration of this has brought up some interesting
questions about the nature of interaction and the measurement problem.
I’ll try and keep this tab updated as and when new things come up.
Quantum-shwantum
 Quantum physics is the prime subject that can
train one to intuitively grasp a description of reality (or a procedural
truth-claims generator) that is not based on our innate
Newtonian/Darwinian instinct. While its predictions are fantastical,
since it is a mathematical theory, all the mystery can be
reduced/collapsed to a handful of (perhaps two) base, quirky phenomena
(not unique). The phenomenological reduction is more suited to teaching,
and readily allows for alternative postulates, representations, and
interpretations to sprout forth. Hence, my interest.
Quantum physics is the prime subject that can
train one to intuitively grasp a description of reality (or a procedural
truth-claims generator) that is not based on our innate
Newtonian/Darwinian instinct. While its predictions are fantastical,
since it is a mathematical theory, all the mystery can be
reduced/collapsed to a handful of (perhaps two) base, quirky phenomena
(not unique). The phenomenological reduction is more suited to teaching,
and readily allows for alternative postulates, representations, and
interpretations to sprout forth. Hence, my interest.
Classical stat-mech
(Coming soon)
 A simple 8:2 mixture of two slightly dissimilar
classical atoms at large enough densities can behave in strange ways
when one attempts to cool them to a low enough temperature. Plotting the
mean-squared displacements of the particles for various timescales
reveals a sluggishness in short-term movement, suggesting a free-energy
barrier. It has been hypothesized that the free-energy landscape for
glass translations is fractalian in feature sizes. Apart from helping to
touch base with undergrad stat-mech, and dealing with efficiently
sampling transient events, this also makes for a great practice problem
to learn parallel GPU programming with.
A simple 8:2 mixture of two slightly dissimilar
classical atoms at large enough densities can behave in strange ways
when one attempts to cool them to a low enough temperature. Plotting the
mean-squared displacements of the particles for various timescales
reveals a sluggishness in short-term movement, suggesting a free-energy
barrier. It has been hypothesized that the free-energy landscape for
glass translations is fractalian in feature sizes. Apart from helping to
touch base with undergrad stat-mech, and dealing with efficiently
sampling transient events, this also makes for a great practice problem
to learn parallel GPU programming with.